Answer:
The given expressions are
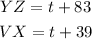
Let the value of

Concept:
We will apply the rule of simolar triangles given below as
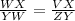
By Substituting the values, we will have
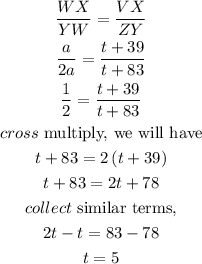
To calculate the value of YZ, we will susbtitute the value of t=5 in the equation below
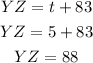
Hence,
The value of YZ = 88