Question

The solution to the exponential equation below has the following general form:t=(logsubb(d/a))divided by c3 x 2^t = 12The question set has four parts. Answer the parts in order:Part 1Substituting the values below into the general form will solve the equation. Whcih value should substitute for a?a) 1b)2c)3d)12Part 2Which value should substitute for b?a) 1b) 2c) 3d) 12Part 3Which value should substitute for c?a) 1b) 2c) 3d) 12Part 4Which value should substitute for d?a) 1b) 2c) 3d) 12

Answer 1

From the problem, we have the equation :

`3\cdot2^t=12`

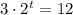
Divide both sides by 3 :

`2^t=(12)/(3)`

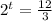
Take the logarithm of both sides :

`\log 2^t=\log (12)/(3)`

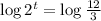
Note that :

`\log m^p=p\log m^{}`

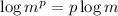
the exponent can be multiplied by the logarithm of m.

So the equation will be :

`\begin{gathered} \log 2^t=\log (12)/(3) \\ t\log 2=\log (12)/(3) \end{gathered}`

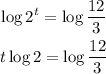
Divide both sides by log 2 so that the left side will only have the variable t.

`t=(\log((12)/(3)))/(\log2)`

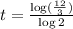
Note that :

`(\log b)/(\log a)=\log _ab`

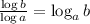
The log of b divided by the log of a is the same as log of b with the base a.

So the equation will be :

`\begin{gathered} t=(\log((12)/(3)))/(\log2) \\ t=\log _2((12)/(3)) \end{gathered}`

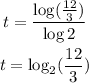
From the problem, it is in the form :

`t=(\log _b((d)/(a)))/(c)=(\log _2((12)/(3)))/(1)`

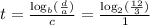
So we can say that :

a = 3, b = 2, c = 1 and d = 12

Answers :

Part 1 : c. 3

Part 2 : b. 2

Part 3 : a. 1

Part 4 : d. 12