From the problem, we have the equation :
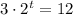
Divide both sides by 3 :
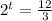
Take the logarithm of both sides :
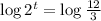
Note that :
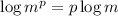
the exponent can be multiplied by the logarithm of m.
So the equation will be :
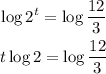
Divide both sides by log 2 so that the left side will only have the variable t.
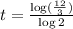
Note that :
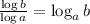
The log of b divided by the log of a is the same as log of b with the base a.
So the equation will be :
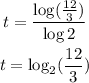
From the problem, it is in the form :
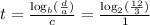
So we can say that :
a = 3, b = 2, c = 1 and d = 12
Answers :
Part 1 : c. 3
Part 2 : b. 2
Part 3 : a. 1
Part 4 : d. 12