Given the roots to be -7 and 1.
Step 1: Equate the roots to x
Hence, the first equation will be
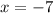
and the second is
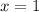
Step 2: Make both expressions be equal to zero
Hence, we have
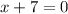
and
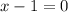
Step 3: Multiply both roots
Hence
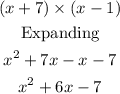
Step 4: The expression gotten from Step 3 should be equated to y.
Hence,
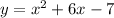
Therefore,