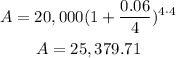Question

Use the compound interest formulas A=P and A=Per to solve the problem given. Round answers to the nearest cent. Find the accumulated value of an investment of $20,000 for 4 years at an interest rate of 6% if the money is a. compounded semiannually, compounded monthly, d. compounded continuously a. What is the accumulated value if the money is compounded semiannually? $ (Round your answer to the nearest cent. Do not include the $ symbol in your answer.) b. What is the accumulated value if the money is compounded quarterly?

Answer 1

`\begin{gathered} a)\text{ }A=25,335.40 \\ b)\text{ }A=25,409.78 \\ c)\text{ }A=25,424.48 \\ d)\text{ }A=25,379.71 \end{gathered}`

Explanation:

Compound interest is represented by the following expression:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ \text{where,} \\ A=\text{ amount} \\ P=\text{ Principal} \\ r=\text{ Interest rate decimal form} \\ n=\text{ number of times interest is compounded per unit t} \\ t=\text{time} \end{gathered}`

Then,

a) Compounded semiannually:

If semi-annually, then n=2.

`\begin{gathered} A=20,000(1+(0.06)/(2))^(2\cdot4) \\ A=20,000(1.03)^8 \\ A=25,335.40 \end{gathered}`

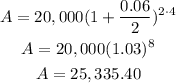
b) Compounded monthly:

If monthly, then n=12

`\begin{gathered} A=20,000(1+(0.06)/(12))^(12\cdot4) \\ A=20,000(1.005)^(48) \\ A=25,409.78 \end{gathered}`

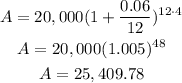
c) Compounded continuously:

If continuously (daily), then n=365

`\begin{gathered} A=20,000(1+(0.06)/(365))^(365\cdot4) \\ A=25,424.48 \end{gathered}`

d) Compounded quarterly:

If quarterly, then n=4.

`\begin{gathered} A=20,000(1+(0.06)/(4))^(4\cdot4) \\ A=25,379.71 \end{gathered}`