Question

The Prices for Graphics Cards for computer systems have been growing dramatically following the exponential growth model in recent years with a rate of growth of 14% per year. This is due to the growth in video game usage as well as video creation and video streaming. For example, the top-of-the-line Gigabyte GEForce RTX graphics card cost $350 new this year ( Po ). a) Write a Recursive Formula P, for the cost of the comparable graphics card in successive years. b) Write an Explicit Formula Py for the cost of the comparable graphics card after N years. c) What is the predicted cost of the comparable graphics card in the year 2025? Show your work. Round final answer to the nearest penny. d) In what year will the cost of the comparable graphics card reach $1000 ? Show your work, including a graph in an Appropriate Window. Label everything appropriately. Give answer accurate to 3 decimal places. {Example of acceptable answer might be: Year=2021.374)

Answer 1

a) We know that each year the price is increased by 14%. That is that the next year price is 1.14 times the actual price.

We can write this as:

`P_(n+1)=1.14\cdot P_n`

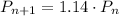
This is a recursive formula because the price depends on the previous prices.

b) If we want to find a explicit formula in function of the years, we need to start from a known price value.

Then, by the recursive formula from the previous point, we can write:

`\begin{gathered} P_1=1.14\cdot P_0 \\ P_2=1.14\cdot P_1=1.14\cdot(1.14\cdot P_0)=1.14^2\cdot P_0 \\ P_3=1.14\cdot P_2=1.14\cdot(1.14^2\cdot P_0)=1.14^3\cdot P_0 \end{gathered}`

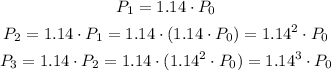
Following that reasoning we can write the explicit formula as:

`P_n=1.14^n\cdot P_0`

c) If the price for 2020 is P0=350, we can use the explicit formula to calculate the value for 2025, that is P5:

`P_5=1.14^5\cdot P_0=1.14^5\cdot350\approx1.925\cdot350\approx673.90_{}`

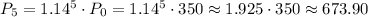
For year 2025, the predicted price is $673.90.

d) We can find when the price will reach $1000 by finding the value of n from the explicit formula.

We can write:

`\begin{gathered} P_n=1.14^n\cdot P_0=1.14^n\cdot350=1000 \\ 1.14^n=(1000)/(350) \\ n\cdot\ln (1.14)=\ln (1000)-\ln (350) \\ n=(\ln (1000)-\ln (350))/(\ln (1.14)) \\ n\approx(6.908-5.858)/(0.131)\approx(1.050)/(0.131)\approx8.012 \end{gathered}`

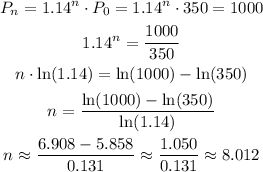
The value for n is 8.012.

As n=0 correspond to 2020, the year where it will reach a price of $1000 is Year=2020+8.012=2028.012.

Answer: Year = 2028.012.