Question

1. The following diagram shows an isosceles trapezold with area of 192 square units and a kite with an area of 136.72 square units. Determine the missing coordinates for the vertex of the trapezoid and the vertex of the kite that is the endpoint of the side that is adjacent to a leg of the trapezold. Write your answers in the boxes shown below. (-12, 4) (-4, 4) It 2x10.02 (4, -8)

Answer 1

We start by calculating the distance between the points (-4, 4) & (4, -8). We find the directional vector and then its dimensions as follows:

`(4-(-4),-8-4)=(8,-12)`

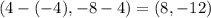
Now that we have the directional vector, we calculate its distance:

`d=\sqrt[]{8^2+(-12)^2}\Rightarrow d=4\sqrt[]{13}`

We also have (Given) that the angular sides in the isosceles trapezoid are congruent and the two sides of the kite are congruent (1 common side) and that the coordinates of the shape have components (a, -8) for the isosceles trapezoid, and (b, 4) for the kite [This is because those coordinates are in the same "level" as the other ones present].

Using the previously mentioned properties and the distance that we calculated, we determine the coordinates of:

*** Coordinate for the missing point in the isosceles trapezoid:

*We determine the directional vector of the points (-12, 4) & (a, -8), that is:

`(a-(-12),-8-4)=(a+12,-12)`

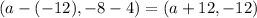
And now, using the distance formula and the distance we calculated before we solve for a as follows:

`4\sqrt[]{13}=\sqrt[]{(a+12)^2+(-12)^2}\Rightarrow208=(a+12)^2+(-12)^2`
`\Rightarrow64=a^2+24a+144\Rightarrow a^2+24a+80=0`

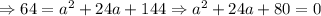
Now, we use the quadratic formula to solve for a:

`a=\frac{-24\pm\sqrt[]{24^2-4(1)(80)}}{2(1)}\Rightarrow a=\begin{cases}a_1=-4 \\ a_2=-20\end{cases}`

From the image we can see that the point is further left than -12, therefore the only solution for this should be -2.

The point that is missing in the isosceles trapezoid is (-20, -8).

*** Coordinate for the missing point in the kite:

Just as the previous point we proceed:

*We determine the directional vector of the points (-4, 4) & (b, 4), that is:

`(b-(-4),4-4)=(b+4,0)`

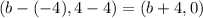
Now, we replace in the distance function:

`4\sqrt[]{13}=\sqrt[]{(b+4)^2+0^2}\Rightarrow208=(b+4)^2`
`\Rightarrow208=b^2+8b+16\Rightarrow b^2+8b-192`

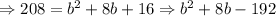
And just as before, we use the quadratic function to solve for b:

`b=\frac{-8\pm\sqrt[]{8^2-4(1)(-192)}}{2(1)}\Rightarrow b=\begin{cases}b_1=-4+4\sqrt[]{13}\Rightarrow b_1\approx10.42 \\ b_2=-4-4\sqrt[]{13}\Rightarrow b_2\approx-18.42\end{cases}`

Since we can see in the picture that the point is to the right of the point (-4, 4) we can see that the only value that meets the parameters is b1 = -4 + 4sqrt(13).

The point that is missing in the kite is (-4+4sqrt(13), 4)