Question

What were the number of photos and price per photo

Answer 1

Step-by-step explanation

Let the quadratic model for the revenue as a function of the number of photos sold be:

`y=ax^2+bx+c`

where y = revenue

x = number of photos sold

a, b, c = constants

Let us substitute the given values of x and y into the equation. This will result in three simultaneous equations:

`\begin{gathered} 180=a(3^2)+b(3)+c \\ \Rightarrow180=9a+3b+c \\ \\ 308=a(7)^2+b(7)+c \\ \Rightarrow308=49a+7b+c \\ \\ 320=a(10)^2+b(10)+c \\ \Rightarrow320=100a+10b+c \end{gathered}`

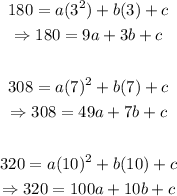
The three equations are:

`\begin{gathered} 9a+3b+c=180 \\ \\ 49a+7b+c=308 \\ \\ 100a+10b+c=320 \end{gathered}`

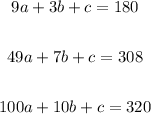
From the first equation, make c the subject of the formula:

`c=180-9a-3b`

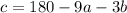
Substitute this equation into the other two equations and simplify.

For the first equation:

`\begin{gathered} 49a+7b+180-9a-3b=308 \\ \\ 40a+4b=308-180 \\ \\ 40a+4b=128 \\ \\ 10a+b=32 \end{gathered}`

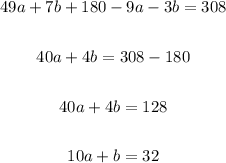
For the second equation:

`\begin{gathered} 100a+10b+180-9a-3b=320 \\ \\ 91a+7b=320-180 \\ \\ 91a+7b=140 \\ \\ 13a+b=20 \end{gathered}`

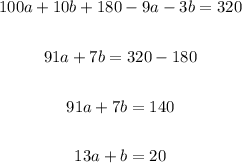
Now, we have another set of two simultaneous equations:

`\begin{gathered} 10a+b=32 \\ \\ 13a+b=20 \end{gathered}`

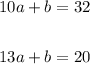
To solve for a, subtract the second equation from the first and simplify:

`\begin{gathered} 10a+b-13a-b=32-20 \\ \\ -3a=12 \\ \\ a=(12)/(-3) \\ \\ a=-4 \end{gathered}`

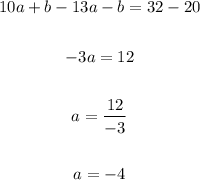
To find the value of b, substitute the value of a into the first equation and solve:

`\begin{gathered} 10(-4)+b=32 \\ \\ -40+b=32 \\ \\ b=32+40 \\ \\ b=72 \end{gathered}`

To find the value of c, substitute the values of a and b into the equation for c and simplify:

`\begin{gathered} c=180-9(-4)-3(72) \\ \\ c=180+36-216 \\ \\ c=0 \end{gathered}`

Therefore, the quadratic model for the revenue is:

`y=-4x^2+72x`

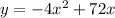
Now, we have to find x when y is the maximum. To do this, find the critical number:

`\begin{gathered} y^(\prime)(x)=0 \\ \\ (dy)/(dx)=-8x+72=0 \\ \\ -8x=-72 \\ \\ x=(-72)/(-8) \\ \\ x=9 \end{gathered}`

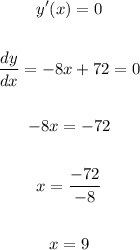
Using the second derivative test, we see that:

`y^(\prime)^(\prime)(x)=-8`

Since -8 < 0, y is maximum when x = 9.

To find the revenue at x = 9, solve for y when x is 9 in the equation for revenue:

`\begin{gathered} y=-4(9)^2+72(9) \\ \\ y=-324+648 \\ \\ y=\$324 \end{gathered}`

To find the price per photo that will maximize the revenue, divide the maximum revenue by the number of photos that will maximize the revenue.

Therefore, the price per photo that will maximize the revenue is:

`\begin{gathered} (324)/(9) \\ \\ \$36\text{ per photo} \end{gathered}`

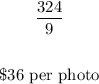
That is the answer.