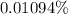Solution:
Since the balls are chosen without replacement, we can apply the hypergeometric distribution. This distribution is given by the following formula:
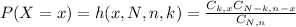
where
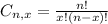
and the parameters are the following:
x is the number of successes.
N is the size of the population.
n is the size of the sample.
k is the total number of desired outcomes.
Now, in this problem we have that:
There are 4 sets of balls numbered 1 through 10 placed in a bowl. This means 4 x 10 = 40 balls, hence N= 40.
On the other hand, for each number, there are 4 balls, hence k = 4.
Finally, we have that 4 balls are selected, thus n= 4.
For each ball, the probability is P(X=4). There are 10 balls, hence we have to find 10 * P(X = 4).
Now, according to the given distribution, we obtain that:
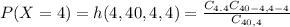
this is equivalent to:
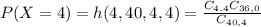
Now, applying the combinatorial formula to the above equation, we obtain:

Thus,
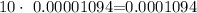
in percent notation, this is equivalent to:
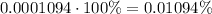
So that, we can conclude that the correct answer is: