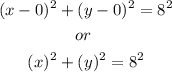The general standard equation for a circle with radius r centered at (h, k) is:
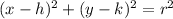
In this problem, since the circle is centered at the origin, the point (h, k) is (0, 0). So, substituting it:
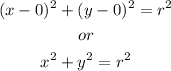
Now, it is only necessary to find the radius. It is given in the picture (x-axis) and it has a value of 8.
So, the equation is: