Question

14. Suppose a math class contains 35 students, 17 females (five of whom speak French) and 18 males (three of whom speak French). Compute the probability that a randomly selected student speaks French, given that the student is male.

Answer 1

The formula to calculate the conditional probability of A given B is given to be:

`P(A|B)=(P(A\cap B))/(P(B))`

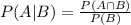
If French is represented by F, and males by M, the formula to calculate the probability of a student speaking French given they are male is given to be:

`P(F|M)=(P(F\cap M))/(P(M))`

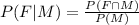
The probability formula is given to be:

`P(A)=(n(A))/(n(T))`

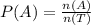
Therefore, we have:

`\begin{gathered} P(F\cap M)=(n(F\cap M))/(n(Students)) \\ n(F\cap M)=students\text{ that speak french and are male}=3 \\ n(Students)=35 \\ \therefore \\ P(F\cap M)=(3)/(35) \end{gathered}`

and

`P(M)=(18)/(35)`

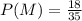
Therefore, the conditional probability is:

`\begin{gathered} P(F|M)=((3)/(35))/((18)/(35))=(3)/(35)*(35)/(18) \\ P(F|M)=(3)/(18)=(1)/(6)=0.167 \end{gathered}`

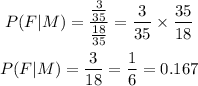
The probability is 0.167 or 1/6