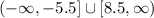The inequality is given as:

STEP 1: Subtract 7 from both sides.
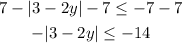
STEP 2: Multiply both sides by -1. This reverses the inequality.
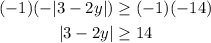
STEP 3: Apply the Absolute Rule.
The Absolute Rule states that:
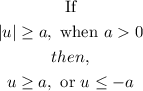
Hence,
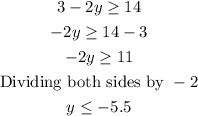
or
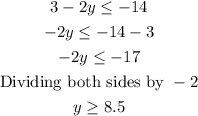
Therefore, the solution is:
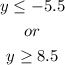
In interval notation, the solution is written out to be: