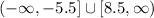Question

Consider the following absolute value inequality. 7 - |3 – 2y| < -7 Step 1 of 2: Solve the inequality and express your answer in interval notation. Use decimal form for numerical values.

Answer 1

The inequality is given as:

`7-|3-2y|\leq-7`

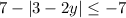
STEP 1: Subtract 7 from both sides.

`\begin{gathered} 7-|3-2y|-7\leq-7-7 \\ -|3-2y|\leq-14 \end{gathered}`

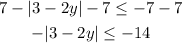
STEP 2: Multiply both sides by -1. This reverses the inequality.

`\begin{gathered} (-1)(-|3-2y|)\ge(-1)(-14) \\ |3-2y|\ge14 \end{gathered}`

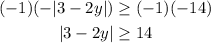
STEP 3: Apply the Absolute Rule.

The Absolute Rule states that:

`\begin{gathered} \text{If} \\ |u|\ge a,\text{ when }a>0 \\ then, \\ u\ge a,\text{ or }u\leq-a \end{gathered}`

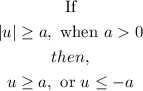
Hence,

`\begin{gathered} 3-2y\ge14 \\ -2y\ge14-3 \\ -2y\ge11 \\ \text{Dividing both sides by }-2 \\ y\leq-5.5 \end{gathered}`

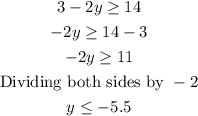
or

`\begin{gathered} 3-2y\leq-14 \\ -2y\leq-14-3 \\ -2y\leq-17 \\ \text{Dividing both sides by }-2 \\ y\ge8.5 \end{gathered}`

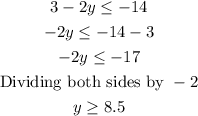
Therefore, the solution is:

`\begin{gathered} y\leq-5.5 \\ or \\ y\ge8.5 \end{gathered}`

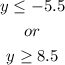
In interval notation, the solution is written out to be:

`(-\infty,-5.5\rbrack\cup\lbrack8.5,\infty)`