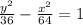Question

A hyperbola has vertices (0,-6) and (0,6) and asymptotes y=3/4 x and y=-3/4 x.Part I: In what direction is this hyperbola oriented? Part II: What are the coordinates of the center of this hyperbola? Part III: What are the values of a and b for this hyperbola? Part IV: Write the equation of this hyperbola.

Answer 1

To help us answer the questions we will plot the vertices and the asymptotes, this is shown below:

Part I:

Since the axis of the hyperbola passes through the vertices we will have a vertical axis in this case; this means that the hyperbola is vertically oriented.

Part II:

The center of the hyperbola is the midpoint of the vertices; the midpoint between two points is given by;

`M((x_1+x_2)/(2),(y_1+y_2)/(2))`

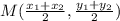
Plugging the vertices (0,-6) and (0,6) on the midpoint formula we have that:

`M((0+0)/(2),(6+(-6))/(2))=M(0,0)`

Therefore, the center of the hyperbola is the point C(0,0)

Part III:

We know that the value of a is the distance from the center to the vertices; in this case, we readily notice that this distance is 6 which means that a=6. Now, we know that the asymptotes of a vertical hyperbola are given by:

`y=\pm(a)/(b)(x-h)+k`

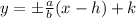
where (h,k) is the center of the hyperbola. In this case we know h=0, k=0 and a=6 then we have:

`y=\pm(6)/(b)x`

Comparing this with the equations given we have:

`\begin{gathered} (6)/(b)=(3)/(4) \\ b=(6)/((3)/(4)) \\ b=8 \end{gathered}`

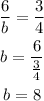
Therefore, a=6 and b=8

Part IV:

The equation of a vertical hyperbola is given by:

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`

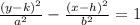
Plugging the values of h, k, a and b we have that:

`\begin{gathered} ((y-0)^2)/(6^2)-((x-0)^2)/(8^2)=1 \\ (y^2)/(36)-(x^2)/(64)=1 \end{gathered}`

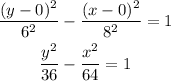
Therefore, the equation of the hyperbola is:

`(y^(2))/(36)-(x^(2))/(64)=1`