Question

If θ is a first quadrant angle in standard position with P(u,v) = (3,4) evaluate cos 2 θ

Answer 1

We have to evaluate cos(2θ), knowing that θ is in the first quadrant and in standard position P(u,v) = (3,4).

We can picture this as:

We can write the relation:

`\tan \theta=(4)/(3)`

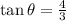
We now look at the identities to find cos(2θ):

`\cos (2\theta)=(1-\tan^2(2\theta))/(1+\tan^2(2\theta))`

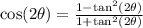
There are many identities for cos(2θ), but this is expressed in the information we already know, so we can solve as:

`\begin{gathered} \cos (2\theta)=(1-\tan^2(2\theta))/(1+\tan^2(2\theta)) \\ \cos (2\theta)=(1-((4)/(3))^2)/(1+((4)/(3))^2) \\ \cos (2\theta)=(1-(16)/(9))/(1+(16)/(9)) \\ \cos (2\theta)=((9-16)/(9))/((9+16)/(9)) \\ \cos (2\theta)=(-7)/(25) \end{gathered}`

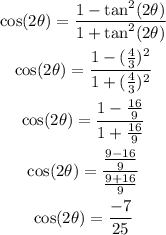
Answer: cos(2θ) = -7/25