Let us make the line from the picture, pointing the given equations:
From the draw and the given equations, we note that:

Therefore, we can solve the equation for y as follows
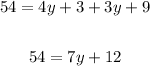
Where in the last line, we add the similar terms, for example 3y+4y=7y. Let us continue the calculations
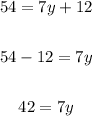
where in the second line of the equation above, we pass the 12 from the right to the left with opposite sign. We discover y as follows
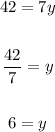
That is, we have y=6.
Let us now calculate the value of RD an RT. We know from the question that

as we discover that y=6, substituting this value in the equations above we find:
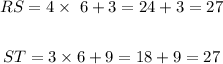
We conclude that RS=27 and ST =27 .