We are asked to determine the average speed of the graph of position vs time. To do that we need to have into account that the average speed is defined as:

Where:
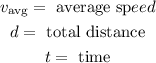
Here, the value of "d" is the total distance that is covered by the particle. Therefore, we need to add the magnitude of the distance that the particle moves. We have the following distances:

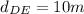

Therefore, the total distance is:
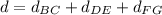
Substituting the values we get:
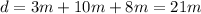
This is the total distance, the total time is:
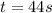
Now we substitute in the formula for the average speed:
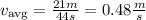
Now we will determine the average velocity. This is given by the following formula:

Where:

The value of the displacement is the difference between the final and initial position, in this case, we have:
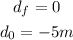
Where:
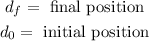
Now we determine the displacement:
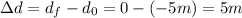
Therefore, the displacement is 5 meters. The change in time is the 44seconds since we are considering the entire graph. Substituting in the formula we get:
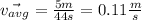
Therefore, the average velocity is 0.11 meters per second.