Question

A 6 kg sign is suspended by two strings making angles with the ceiling as shown in the diagram. Determine the magnitudes of the tensions in each string. Remember that 1kg exerts a force of 9.8 N. please use sine/cosine when answering

Answer 1

From the diagram given we have that the free body diagram of the forces acting on the sign is:

We know that the weight of the sign is given by:

`W=mg`

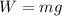
where m is the mass and g is the acceleration of gravity (9.8 m/s²), then the weight is:

`\begin{gathered} W=(6)(9.8) \\ W=58.8 \end{gathered}`

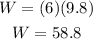
Now, we know that Newton's second law states that:

`\vec{F}=m\vec{a}`

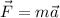
where F is the resultant force acting on the object, m is its mass and a is the acceleration. This is a vector equation, since we have a two dimensional problem, this means that this equation will be equivalent to two scalar equations, one for each direction. Newton's second law in two dimensions can then be written as:

`\begin{gathered} F_x=ma_x \\ F_y=ma_y \\ \text{ where} \\ F_x\text{ is the x-component of the resultant force } \\ F_y\text{ is the y-component of the resultant force } \\ a_x\text{ is the x-component of the acceleration} \\ a_y\text{ is the y- component of the accelerat}\imaginaryI\text{on} \end{gathered}`

Now, to get the components of the resultant force we need to add the components of the forces acting on the object; we know that a vector is decompose in its rectangular components as:

`\begin{gathered} \vec{F}=\langle F\cos\theta,F\sin\theta\rangle \\ \text{ where } \\ F\text{ is the magnitude of the vector } \\ \theta\text{ is the direction of the vector \lparen the angle measure from the positive x-axis\rparen} \end{gathered}`

Let's decompose each force. For tension 1 the angle is 67°, then we have:

`\vec{T}_1=\langle T_1\cos67,T_1\sin67\rangle`

For tension 2 the angle is 180°-48°=132°, then we have:

`\vec{T}_2=\langle T_2\cos132,T_2\sin132\rangle`

Finally for the weight the angle is 270°, then:

`\begin{gathered} \vec{W}=\langle58.8\cos270,58.8\sin270\rangle \\ \vec{W}=\langle0,-58.8\rangle \end{gathered}`

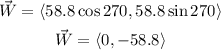
Note: In the case of the weight we readily from the diagram that it points in the negative y-direction.

Now that we have all the vector in component form we can add them to find the resultant force:

`\vec{T}__1+\vec{T}_2+W=\langle T_1\cos67+T_2\cos132+0,T_1\sin67+T_2\sin132-58.8\rangle`

Which means that:

`\begin{gathered} F_x=T_1\cos67+T_2\cos132 \\ F_y=T_1\sin64+T_2\cos132-58.8 \end{gathered}`

Plugging these values in our equations of motion we have:

`\begin{gathered} T_1\cos67+T_2\cos132=ma_x \\ T_1\sin67+T_2\sin132-58.8=ma_y \end{gathered}`

Now, since the sign is in equilibrium, its acceleration is zero which means that the equations above lead to:

`\begin{gathered} T_1\cos67+T_2\cos132=0 \\ T_1\sin67+T_2\sin132=58.8 \end{gathered}`

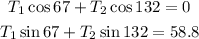
This is a system of equations that we can solve to find the tensions; to do this we solve the first equation for one of the tensions and we plug it in the second equation which will lead to an equation with only one variable that we can readily solve. Let's do this for tension 1; from the first equation we have:

`\begin{gathered} T_1\cos67+T_2\cos132=0 \\ T_1\cos67=-T_2\cos132 \\ T_1=-(\cos132)/(\cos67)T_2 \end{gathered}`

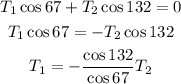
Let's plug this in the second equation and solve the resulting equation for tension 2:

`\begin{gathered} (-(\cos132)/(\cos67)T_2)(\sin67)+T_2\sin132=58.8 \\ T_2(-\cos132\tan67+\sin132)=58.8 \\ T_2=(58.8)/(-\cos132\tan67+\sin132) \\ T_2=25.35 \end{gathered}`

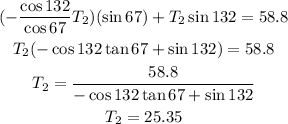
Now that we have tension 2 we can plug its value in our expression for tension 1:

`\begin{gathered} T_1=-(\cos132)/(\cos67)(25.35) \\ T_1=43.41 \end{gathered}`

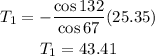
Therefore, tension one is 43.41 N and tension two is 25.35 N