Question

The sum, Sn, of the first n terms of an arithmetic sequence is given by Sn = 2 (a, + an), in which a, is the first term and an is the nth term. The sum S, of the firsta, (1-")terms of a geometric sequence is given by S. =-1-1in which a, is the first term and is the common ratio (r+ 1). Determine whether the following sequencearithmetic or geometric. Then use the appropriate formula to find S10, the sum of the first ten terms.3.9.15, 21Determine whether the sequence is arithmetic or geometřic. Choose the correct answer below.ArithmeticGeometricS10=0Click to select your answers)

Answer 1

`\begin{gathered} S_n=(n)/(2)(a_1+a_n)\ldots\ldots\ldots\ldots\ldots\text{ arithmetic sequence } \\ S_n=(a_1\mleft(1-r^n\mright))/(1-r)\ldots\ldots\ldots\ldots\ldots\text{.geometric sequence} \\ \end{gathered}`

The sequence; 3, 9, 15, 21.

Now, from the definition of both sequence, A sequence is an arithmetic if it has a common difference. And a sequence is geometric if it has a common ratio.

A common difference d, is thus given as;

`d=a_2-a_1=\text{ }a_3-a_2`

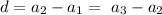
While a common ratio r, is given as;

`r=(a_2)/(a_1)=(a_3)/(a_2)`

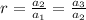
So, testing for the one that satisfy the sequence, we observed that;

`\begin{gathered} 21-15=15-9=9-3=6 \\ \text{That is, it has a common difference.} \end{gathered}`

Thus, the sequence ia an arithmetic sequence.

Before we can find the Sum of the first ten terms, we have to get the tenth term;

`\begin{gathered} a_n=a_1+(n-1)d \\ \text{Where d=common difference} \\ a_(10)=\text{ tenth term} \\ a_1=\text{ first term} \\ n=\text{number of term} \\ a_(10)=3+(10-1)(6)=3+54=57 \end{gathered}`

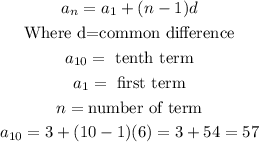
Then;

`\begin{gathered} S_(10)=(10)/(2)(3+57) \\ S_(10)=5(60) \\ S_(10)=300 \end{gathered}`

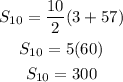
Thus, the sum of the first ten terms is 300.