Question

Hi I’ve been struggling with these three problems for a while now

Answer 1

The segment addition postulate states that if we are given two points on a line segment, A and C, a third point B lies on the line segment AC if and only if the distances between the points meet the requirements of the equation AB + BC = AC.

Also, line segment AB is the same as line segment BA as it passes through the same two points A and B. Therefore we can conclude that the length of the line segment bound between two points stays the same, even if the points are reversed. Hence, segment AB is equal to segment BA.

Part A:

Applying the segment addition postulate,

`\begin{gathered} CB+BD=CD \\ \\ \text{But CB=BC} \\ \text{Given:} \\ BC=CB=10in \\ BD=3in \\ CD=? \\ \text{Thus;} \\ 10+3=CD \\ CD=13in \end{gathered}`

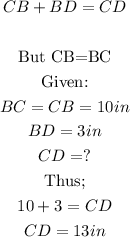
Therefore, CD is 13in

Part B:

Applying the segment addition postulate,

Therefore, QT = 18cm

Part C:

Applying the segment addition postulate,

`\begin{gathered} LP+PA=LA \\ \\ \text{But LP}=PL \\ \text{Given:} \\ PL=LP=x+4 \\ PA=2x-1 \\ LA=5x-3 \\ \text{Thus;} \\ (x+4)+(2x-1)=5x-3 \\ \text{Collecting the like terms and solving for x,} \\ x+2x-5x=-3-4+1 \\ -2x=-6 \\ \text{Dividing both sides by -2;} \\ x=(-6)/(-2) \\ x=3 \end{gathered}`

Therefore, x = 3.

`\begin{gathered} LA=5x-3 \\ \text{Substituting x into LA,} \\ LA=5(3)-3 \\ LA=15-3 \\ LA=12 \end{gathered}`

Therefore, LA = 12