We will have the following:
From the problem we obtain the following expressions:
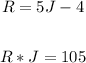
Now, we will determine the ages, that is:
First, we replace the value of "R" in the second expression:
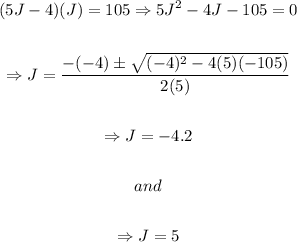
Now, since it would certainly make little sense to have a negative age we will take the positive value for Joshua's age, then:
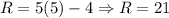
So, Ryan's age is 21 and Joshua's age is 5.
***Explanation***
We are told that Ryan's age is 4 less than 5 times Joshua's age. So, we can write Ryan's age in terms of Joshua's, that is:
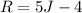
Here "R" is Ryan's age and "J" is Joshua's age.
We are also told that the product of their ages is 105. This can be expressed as:
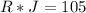
But we remember that Ryan's age can be written in terms of Joshua's age, and so, we obtain that:
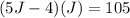
Now, we expand this expression, that is:
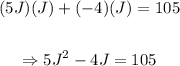
From this, we can see that it can be written as the general quadratic form, that is:

And thus, we can solve for "J" using the quadratic formula.
Note: Quadratic formula:
For a quadratic function that follows:

We can solve for the variable using the quadratic formula, that is:

And thus two solutions will be obtained:
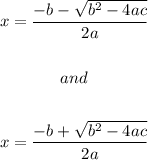
Now that we have recalled the quadratic formula, we will solve for the expression at hand:

That is:
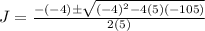
So, the two solutions will be:
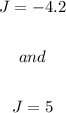
So, we have two values that can be used; but since a negative age makes no sense we only use the positive value; from this we can conclude that Joshua's age is 5 years.
Now that we know Joshua's age, we can replace it in Ryan's expression in terms of Joshua's age, that is:
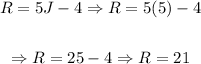
So, from this we can see that Ryan's age is 21 years.