Question

Given the following exponential function, identify whether the change represents growth or decay, and determine the percentage rate of increase or decrease. y = 2000(1.04) Submit Answer |Growth % increase temption

Answer 1

You have the following exponential function:

`y=2000(1.04)^x`

due to the number inside the parenthesis is greater than 1, for greater values of x, the values oy also increase. Hence, the function growths.

To determine the rate of increase, calculate the value of y for x = 0 and the value of y for x = 1, and then compare the values of y:

`\begin{gathered} y=2000(1.04)^0=2000(1)=2000 \\ y=2000(1.04)^1=2000(1.04)=2080 \end{gathered}`

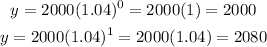
the difference between the previous values is 80, this corresponds to the following percentage:

`\begin{gathered} (x)/(100)(2000)=80 \\ x=(80(100))/(2000) \\ x=4 \end{gathered}`

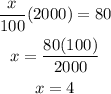
The rate of increase is 4%