Question

In the accompanying diagram of circle O, chords AB and CD intersect at E andAC:CB:BD:DÀ= 4:2:6:8What is the measure of AC, BD, and angle DEB?

Answer 1

arc AC = 72°

arc BD = 108°

∠DEB = 90°

Step-by-step explanation:

AC:CB:BD:DA = 4:2:6:8

ratio of AC = 4

ratio of CB = 2

ratio of BD = 6

ratio of DA = 8

Total ratio = 4 + 2 + 6 + 8 = 20

Total angles in a circle = 360°

`\begin{gathered} arcAC=\frac{ratio\text{ of AC}}{total\text{ ratio}}*360\degree \\ \text{arc AC = }(4)/(20)*360\text{ =}(1440)/(20) \\ \text{arc AC = }72\degree \end{gathered}`
`\begin{gathered} \text{arc BD = }\frac{ratio\text{ of BD}}{\text{total ratio}}*360\degree \\ \text{arc BD = }(6)/(20)*360\degree\text{ =}(2160)/(20) \\ \text{arc BD = 108}\degree \end{gathered}`

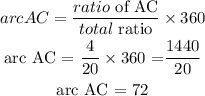
Intersecting chord theorem:

∠DEB = 1/2(arc BD + arc AC)

∠DEB = 1/2(108 + 72)

∠DEB = 1/2(180)

∠DEB = 90°