arc AC = 72°
arc BD = 108°
∠DEB = 90°
Step-by-step explanation:
AC:CB:BD:DA = 4:2:6:8
ratio of AC = 4
ratio of CB = 2
ratio of BD = 6
ratio of DA = 8
Total ratio = 4 + 2 + 6 + 8 = 20
Total angles in a circle = 360°
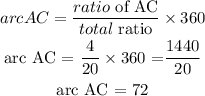
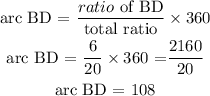
Intersecting chord theorem:
∠DEB = 1/2(arc BD + arc AC)
∠DEB = 1/2(108 + 72)
∠DEB = 1/2(180)
∠DEB = 90°