Question

Solve sin(2x+1.5)=−0.3 for 0≤x≤2π, giving your answer in radians correct to 2 decimal places.(Write the angles in ascending order)

Answer 1

Trigonometric Equations

Solve:

`\sin (2x+1.5)=-0.3\text{ for }0\le x\le2\pi`

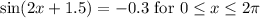
We'll do the calculations with a precision of 4 decimal places throughout the procedure, but we'll round to 2 decimal places when giving the results.

To solve this equation, we need a scientific calculator or any other calculating device or app (like Excel) and it must be set to radians.

To solve for x, we first need to use the inverse sine function:

`2x+1.5=\arcsin (-0.3)`

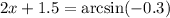
Now we subtract 1.5:

`2x=\arcsin (-0.3)-1.5`

Divide by 2:

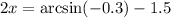
`x=(\arcsin (-0.3)-1.5)/(2)`

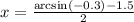
The expression above is the exact solution, but it's required to give the answer in radians, so we must evaluate it.

When we enter arcsin(-0.3) in our calculator, it returns -0.3047 (in radians).

This value is not between the required limits, so we must add 2π to convert it to a positive angle in the same position, thus:

arcsin(-0.3) = -0.3047 + 2π = 5.9785 rad

But this is not the only angle whose sine is -0.3. There is another angle in Quadrant III with the same value of the sine. We find it by subtracting the original angle from π radians:

arcsin(-0.3) = π - (-0.3047) = 3.4463 radians

We now have the two angles whose sine is -0.3, but we must add 2π to find them in the next rotation because the variable x comes with a coefficient of 2 and we could miss some solutions if we didn't.

Thus, the other two solutions for arcsin(-0.3) are:

arcsin(-0.3) = 5.9785 + 2π = 12.2617 radians

arcsin(-0.3) = 3.4463 + 2π = 9.7295 radians

Now substitute all four results in the general solution:

`\begin{gathered} x=(5.9785-1.5)/(2) \\ x=2.24rad \end{gathered}`
`\begin{gathered} x=(3.4463-1.5)/(2) \\ x=0.97rad \end{gathered}`
`\begin{gathered} x=(12.2617-1.5)/(2) \\ x=5.38rad \end{gathered}`
`\begin{gathered} x=(9.7295-1.5)/(2) \\ x=4.11rad \end{gathered}`

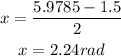
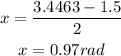
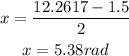
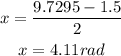
In ascending order:

x = 0.97 rad

x = 2.24 rad

x = 4.11 rad

x = 5.38 rad

Note: All of the solutions are in the required range.