Question

Use the distance formula to calculate the length of side CD and DA

Answer 1

Given the line segment with endpoints DC

Step 1: Write the coordinates of the points and define the (x,y) values

`\begin{gathered} D(1,-2),x_1=1,y_1=-2 \\ C(4,-1),x_2=4,y_2=-1 \\ \end{gathered}`

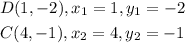
Step 2: Write the formula for the distance between two points

`\begin{gathered} |DC|=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \end{gathered}`

Step 3: Substitute the x and y values

`\begin{gathered} |DC|=\sqrt[]{(4-1)^2+(-1-(-2)_{})^2} \\ =\sqrt[]{(3^2)+(1)^2} \\ =\sqrt[]{9+1} \\ =\sqrt[]{10}\text{ units =3.16units} \end{gathered}`

Hence, the length of the DC is 3.16 units

Or

`\sqrt[]{10}\text{ units}`

Step 4: Use similar procedure for side CD above to obtain side DA

`\begin{gathered} A(-2,2),x_1=-2,y_1=2 \\ D(1,-2),x_2=1,y_2=-2 \end{gathered}`
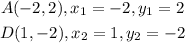
`\begin{gathered} |AD|=\sqrt[]{(1-(-2_{}_{}))^2+(-2-2)^2} \\ =\sqrt[]{(1+2)^2+(-4)^2} \\ =\sqrt[]{3^2+16} \\ =\sqrt[]{9+16^{}} \\ =\sqrt[]{25\text{ }}\text{ =5 units} \end{gathered}`

`\begin{gathered} |AD|=\sqrt[]{(1-(-2))^2+(-2-2)^2_{}} \\ =\sqrt[]{(1+2)^2+(-4^2)} \\ =\sqrt[]{9+16} \\ =\sqrt[]{25} \\ =5\text{units} \end{gathered}`

Hence the length of side DA is 5 units

Summary

CD =3.16 units or root 10

DA= 5 units