Solution
- The decay of the substance is governed by the following function:
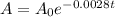
- We are asked to find the half-life of the substance.
- The half-life of the substance is the time it takes for the substance to decay from its original mass to half its original mass.
- Based on this definition, we can say that:
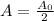
- Thus, we can find the half-life as follows:

Final Answer
The half-life is 247.55 hours