Question

Solve 6x3 − 11x2 − 4x + 4 = 0 by factoring

Answer 1

The polynomial is given below as

`6x^3-11x^2-4x+4=0`

Step 1:The polynomial can be factorized by using the rational root test. To apply this test first we need to find at least one rational zero.

From the root test, we can deduce that

`\begin{gathered} (x-2)=0 \\ x=2 \end{gathered}`

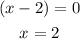
Check:

`\begin{gathered} 6x^3-11x^2-4x+4=0 \\ 6(2)^3-11(2)^2-4(2)+4 \\ 6(8)-11(4)-8+4 \\ 48-44-8+4 \\ 4-8+4 \\ =0 \end{gathered}`

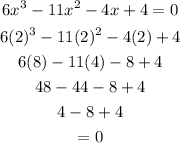
Is a factor of the polynomial above

Step 2:Divide

`6x^3-11x^2-4x+4=0`

By

`(x-2)`

Using the synthetic division, we will have the quotient of the division be

From the steps above, we can see that

`(6x^3-11x^2-4x+4)/(x-2)=6x^2+x-2`

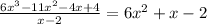
That is,

`6x^3-11x^2-4x+4=(x-2)(6x^2+x-2)`

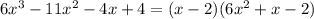
Step 3: Factorize the quadratic expression below

`6x^2+x-2`

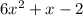
To do this, we will have to look for two factors that will give a product of (6^-2 =-12) and the same two factors that will give a sum of +1

Using the try and error method, the two factors are

`\begin{gathered} +4*-3=-12 \\ +4-3=+1_{} \end{gathered}`

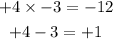
Replace +x with the +4x-3x below as

`\begin{gathered} 6x^2+x-2 \\ 6x^2+4x-3x-2 \\ 2x(3x+2)-1(3x+2) \\ (3x+2)(2x-1) \end{gathered}`

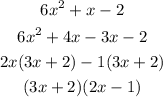
Hence,

`6x^3-11x^2-4x+4=(x-2)(3x+2)(2x-1)=0`

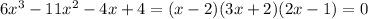
To find the zeros, we will equate each factor to be =0

`\begin{gathered} (x-2)(3x+2)(2x-1)=0 \\ x-2=0,3x+2=0,2x-1=0 \\ x=2,3x=-2,2x=1 \\ x=2,x=-(2)/(3),x=(1)/(2) \end{gathered}`

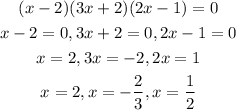
Therefore,

The final values for x are

x=2

x= -2/3

x=1/2