Answer:
16.7 inches
Explanation:
Given:
• Length of an arc = 10 inches
,
• The angle subtended at the center = 0.6 radians
We are required to find the length of the radius.
The length of an arc, s is calculated using the formula:

Substitute the given values:
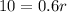
Divide both sides by 0.6:
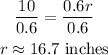
The length of the radius is 16.7 inches (correct to the nearest tenth of an inch).