Recall:

If z varies directly with x, that will be z = kx
If z varies inversely with y, that will be z = k/y
Combining the two equations, we get:
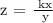
We will be using the first set of values to solve for the constant of variation k.
At x = 2, y = 5 and z = 10,
We get,
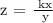
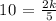
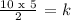

Now apply the constant k with the second values to solve for z.
At x = 3 and y = 15,
We get,
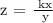

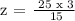

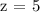
Therefore, z = 5