Given that,
The mass of marble A, m₁=0.08 kg
The mass of marble B, m₂=0.05 kg
The initial velocity of marble A, u₁=0.5 m/s
As the marble B was at rest, the initial velocity of marble B is u₂=0 m/s
The final velocity of marble A, v₁=-0.1 m/s
Let the final velocity of marble B be v₂.
According to the law of conservation of momentum, the total momentum before the collision is equal to the total after the collision.
Therefore
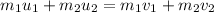
On rearranging the above equation,
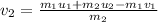
On substituting the known values in the above equation,
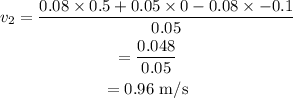
Therefore the