The slope of the line that passes through the points (x1, y1) and (x2, y2) is computed as follows:

The line passes through the points (3, -6) and (-6, -3), its slope is:

The slope-intercept form of a line is:
y = mx + b
where m is the slope and b is the y-intercept.
Substituting with m = -1/3 and the point (3, -6), we get:
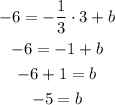
The equation is:
y = -1/3x - 5
To graph a line, you need to find 2 points on it and connect them. Using the points (3, -6) and (-6, -3), we get: