Question

A population of a certain species of bat is 8,000 animals and is increasing at the rate of 5% per year.Write an equation for y , the population at time t (in years), representing the situation. Y=How many bats are in the population after 12 years?

Answer 1

In this problem, we have an exponential growth function

`y=a(1+r)^x`

where

y is the population of bats

r is the rate

a is the initial value

x is the number of years

so

a=8,000

r=5%=5/100=0.05

substitute

`\begin{gathered} y=8,000(1+0.05)^x \\ y=8,000(1.05)^x \end{gathered}`

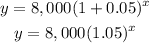
For x=12 years

`\begin{gathered} y=8,000(1.05)^(12) \\ y=14,367\text{ bats} \end{gathered}`

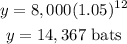
The answer is 14,367 bats (rounded to the nearest whole number)