Given:
In a table,
x values are -2, -1, 0, 1, 2.
y vales are 25, 5, 1, 1/5, 1/25
The objective is to prove whether the table values represents an exponential function or not. And also to find the rule for the function.
Consider the x values in the given table. The difference between each value will be,
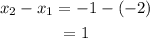
Similarly,
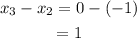
Thus, the values of x are constantly increasing with positive 1 unit.
Consider the y values in the given table.
Te ratio between each term will be,
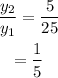
Similarly,
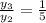
Thus, there is a common ratio between each values of y in the table.
So, it is clear with the common ratio, that the given table value is an exponential functiton.
Now, the rule for the function can be written as,
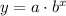
Consider the coordinate, (x,y) = (0,1) and substitute in the above formula.
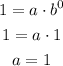
Consider another coordinate (1, 1/5) and the value of a. Substitute the obtained values in the general formula.

Now, substitue only the value of a and b in the general formula.
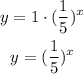
Hence, the rule for the given exponential function is y=(1/5)^x.