We are given the following function:
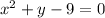
We are asked to determine the intercepts of the function.
To determine the y-intercept we will set "x = 0", we get:
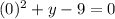
Now, we solve the operations:
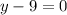
Now, we add 9 to both sides:
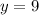
Therefore, the y-intercept is located at "y = 9".
To determine the x-intercept we will set "y = 0":
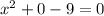
Now, we solve the operations:
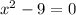
Now, we add 9 to both sides:
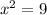
Taking the square root to both sides_:
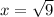
Solving the operations:

This means that there are two x-intercepts:

To test for symmetry with respect to the y-axis we will substitute "x" for "-x" if we get the same function then there is symmetry with respect to "y".
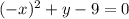
Solving we get:
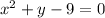
Since we got the same function this means that there is symmetry with respect to the y-axis.
To determine if there is symmetry with respect to the x-axis we will substitute the value of "y" for "*-y":
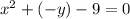
Now, we solve the operations:
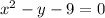
Since we get a different function there is no symmetry with respect to the x-axis.
To determine if there is symmetry with respect to the origin we will substitute "x" and "y" for "-x" and "-y":
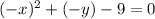
Solving the operations:
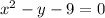
Since we didn't get the same function there is no symmetry with respect to the origin.