Question

The figures to the right are similar. Compare the first figure to the second. Give the ratio of the perimetersand the ratio of the areas.The ratio of the perimeters is .(Type an integer or a simplified fraction.)The ratio of the areas is(Type an integer or a simplified fraction.)Enter your answer in each of the answer boxes.

Answer 1

It is given that the figures are similar:

The ratio of heights is same as the ratio of bases:

`(h_1)/(h_2)=(b_1)/(b_2)=(36)/(45)=(4)/(5)`

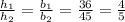
Use theorem of equal ratios to get:

`(h_1)/(h_2)=(b_1)/(b_2)=\frac{b_1+h_1}{b_2+h_2^{}}=(4)/(5)`

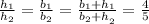
Therefore the formula of perimeter is given by:

`P=2(b+h)`

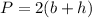
Therefore it follows:

`\begin{gathered} (P_1)/(P_2)=(2(b_1+h_1))/(2(b_2+h_2)) \\ (P_1)/(P_2)=((b_1+h_1))/((b_2+h_2)) \\ (P_1)/(P_2)=(4)/(5) \end{gathered}`

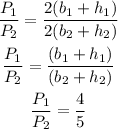
The ratio of areas is given by:

`\begin{gathered} (A_1)/(A_2)=(b_1h_1)/(b_2h_2) \\ (A_1)/(A_2)=(4)/(5)*(4)/(5) \\ (A_1)/(A_2)=(16)/(25) \end{gathered}`

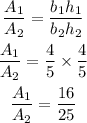
Hence the ratio of perimeters is 4/5 and ratio of areas is 16/25.