It is given that the figures are similar:
The ratio of heights is same as the ratio of bases:
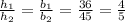
Use theorem of equal ratios to get:
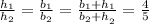
Therefore the formula of perimeter is given by:
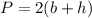
Therefore it follows:
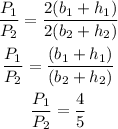
The ratio of areas is given by:

Hence the ratio of perimeters is 4/5 and ratio of areas is 16/25.