The horizontal position of the arrow x(t) and its vertical position y(t) as functions of time, if the arrow is thrown horizontally and if we consider that the arrow starts at the origin of the coordinate system, are given by the expressions:
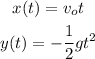
Let t be the time at which the arrow hits 48.0 cm lower than the center of the target.
In that moment, the vertical position of the arrow is -48.0 cm. Replace y(t)=-48.0cm and the value of the gravitational acceleration, g=9.81m/s^2, to find the time that it takes for the arrow to reach that position:
![\begin{gathered} y(t)=-(1)/(2)gt^2 \\ \Rightarrow-48.0\operatorname{cm}=-(1)/(2)(9.81(m)/(s^2))t^2 \end{gathered}]()
Solve for t:
![\begin{gathered} \Rightarrow-(1)/(2)t^2=(-48.0cm)/(9.81(m)/(s^2)) \\ \Rightarrow t^2=(-2*(-48.0cm))/(9.81(m)/(s^2)) \\ \Rightarrow t^2=(2*(0.480m))/(9.81(m)/(s^2)) \\ \Rightarrow t=\sqrt[]{(2*(0.480m))/(9.81(m)/(s^2))} \\ \therefore t=0.3128247548\ldots s \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/kf442t5ks0hdbf7ktkx03f28j3745ra5tk.png)
At the same time, the horizontal position of the arrow is equal to 16.0m.
Replace this value for the horizontal position of the arrow and the value of the time to find the initial speed of the arrow:

Therefore, the initial speed of the arrow was approximately 51.1 meters per second.