Question

Find an equation of the tangent line to the graph of the function at the given point.

Answer 1

We will have the following:

First, we determine the derivative of the expression, that is:

`y=9ln((e^x+e^(-x))/(2))\Rightarrow y^(\prime)=(9(e^(2x)-1))/(1+e^(2x))`

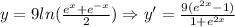
Now, we determine the value of the slope at x = 0, that is:

`y^(\prime)(0)=(9(e^(2(0))-1))/(1+e^(2(0)))\Rightarrow y^(\prime)(0)=(9(1-1))/(1+1)\Rightarrow y^(\prime)(0)=0`

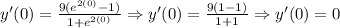
So, from this we will have that the equation of the line that is tangent for the function at the point (0, 0) will be:

`y-0=0(x-0)\Rightarrow y=0`

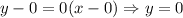
So, the equation of the line will be:

`y=0`

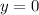
This can be seeing as follows: