We will have the following:
First, we determine the derivative of the expression, that is:
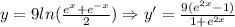
Now, we determine the value of the slope at x = 0, that is:
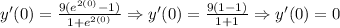
So, from this we will have that the equation of the line that is tangent for the function at the point (0, 0) will be:
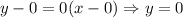
So, the equation of the line will be:

This can be seeing as follows: