Question

Find the equation of the line in slope-intercept form through (6, 1) and perpendicular to Y= 3 / 2 X + 1/4

Answer 1

The general form of the equation of a line in slope intercept is y = mx+b where m is the slope and b is the intercept. To find the equation, we simply need to find the values of m and b.

Have in mind that if we have two lines y = mx+b and y = dx+e, we say that two lines are perpendicular if the product of their slopes is -1. That is

`m\cdot d\text{ = -1}`

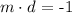
We are given the line y = (3/2)x+(1/4). For this line, the slope is (3/2). Since we want that our line y =mx+b is perpendicular to the given line, it must happen that

`m\cdot((3)/(2))\text{ = -1}`

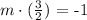
If we multiply by 2 on both sides and then divide by 3, we get

`m\text{ = -1}\cdot(2)/(3)=-(2)/(3)`

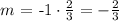
So far, we have the equation of our line to be y = (-2/3)x+b. We are given that this line passes through the point (6,1). This means that in this equation, if we replace x by 6, then we get y=1. This leads to the equation

`1=(-(2)/(3))\cdot6+b\text{ = -2}\cdot2+b\text{ = -4+b}`

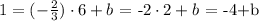
So, if we add 4 on both sides, we get

`b\text{ = 1+4 = 5}`

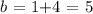
So the equation of our line is y = (-2/3)*x + 5.