Question

The state education commission wants to estimate the fraction of 10th grade students that have reading skills at or below the eighth grade level. In an earlier study the population proportion was estimated to be 0.22 How large of a sample would be required in order to estimate the fraction of 10th graders reading at or below the eighth grade level at the 85% confidence level with an error of at most 0.03? Round your answer up to the next integer

Answer 1

INFORMATION:

We know that:

- In an earlier study, the population proportion was estimated to be 0.22

And we must calculate how large of a sample would be required in order to estimate the fraction of 10th graders reading at or below the eighth grade level at the 85% confidence level with an error of at most 0.03

STEP BY STEP EXPLANATION:

To calculate it, we need to use the following formula

`E=Zc*\sqrt{(p(1-p))/(n)}`

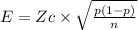
Where,

- E is the margin of error

- Zc is the value from Zc table based on the level of confidence

- p is the population proportion

- n represents the sample

From given information,

- E = 0.03

- p = 0.22

- Using the table for Zc values, we know that for this case Zc = 1.44

Now, we must replace the values in the equation and solve it for n

`\begin{gathered} 0.03=1.44*\sqrt{(0.22(1-0.22))/(n)} \\ (0.03)/(1.44)=(√(0.22(0.78)))/(√(n)) \\ √(n)*0.03=√(0.22(0.78))*1.44 \\ √(n)=(0.5965)/(0.03) \\ √(n)=19.8833 \\ n=(19.8833)^2 \\ n=395.3456 \end{gathered}`

Since n refers to students, we must round the answer to the next whole number.

Finally, the sample must be of 396 students.

ANSWER:

396