Question

One inlet pipe can fill an empty pool in 16 hours, and a drain can empty the pool in 20 hours. How long will it take the pipe to fill the pool if the drain is left open? hours

Answer 1

The situation can be expressed in an equation system

Let V be the total volume of the pool, then

`\begin{gathered} 16x=V \\ 20y=V \end{gathered}`

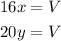
with x, y in volume per time (x is the speed with which the pool is being filled, y the speed with which the water is being drained)

`\begin{gathered} \Rightarrow16x=20y \\ \Rightarrow(y)/(x)=(16)/(20)=(4)/(5) \\ \Rightarrow y=(4)/(5)x \end{gathered}`

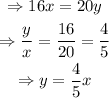
So, the speed with which the water escapes from the pool is 4/5 of the speed with which the pool is being filled

`\begin{gathered} t(x-y)=V \\ \Rightarrow t(x-(4)/(5)x)=V \\ \Rightarrow t((1)/(5)x)=V \end{gathered}`

Then,

`\begin{gathered} t=(V)/(((1)/(5)x)), \\ \text{but 16x=V} \\ \Rightarrow t=(16x)/(((1)/(5)x)) \\ \Rightarrow t=(16)/((1)/(5))=16\cdot5=80 \end{gathered}`

Therefore, the pool will be completely filled in 80 hours