The situation can be expressed in an equation system
Let V be the total volume of the pool, then
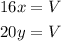
with x, y in volume per time (x is the speed with which the pool is being filled, y the speed with which the water is being drained)
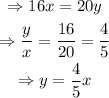
So, the speed with which the water escapes from the pool is 4/5 of the speed with which the pool is being filled
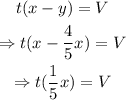
Then,
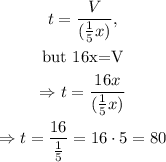
Therefore, the pool will be completely filled in 80 hours