Question

Consider the following equation:64x^4– 25x^2 = 0Step 1 of 2: Completely factor the left-hand side of the equation into two or more factors.Step 2 of 2: Solve the given equation by factoring. separate multiple solutions with a comma.

Answer 1

Step 1: x²(8x + 5)(8x - 5) = 0

Step 2: x = 0, -5/8, 5/8

Step-by-step explanation:

The initial expression is:

`64x^4-25x^2=0`

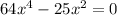
First, we can factorize x², so we can rewrite the expression as:

`\begin{gathered} (64x^2\cdot x^2)-(25\cdot x^2)=0 \\ x^2(64x^2-25)=0 \end{gathered}`

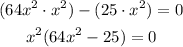
Now, (64x² - 25) is a difference of squares because 64x² = (8x)² and 25 = 5². Therefore, they can be factorized as:

`x^2(8x+5)(8x-5)=0`

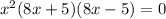
Therefore, the completely factored equation is:

x²(8x + 5)(8x - 5) = 0

Then, this equation is equal to 0 if at least one of the factors is 0, so the solutions of the equation are:

x² = 0

x = 0

8x + 5 = 0

8x + 5 - 5 = 0 - 5

8x = -5

8x/8 = -5/8

x = -5/8

8x - 5 = 0

8x - 5 + 5 = 0 + 5

8x = 5

8x/8 = 5/8

x = 5/8

So, the solutions of the equation are:

x = 0, -5/8, 5/8