We have a number of two digits that we call xy, we know that x+y=14 and yx-xy=18.
Due x and y could be integers between 0 and 9, we can write the following equations:

The second equation represent the condition that yx-xy=18, to satisfy that condition we assume that y borrow an unit to x so 1x-y=8, so (y-1)-x=1.
Now, we solve the equations:
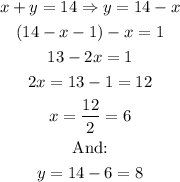
So, the number is 68, and 86-68=18.