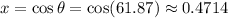Answer: x ≈ 0.4714
Step-by-step explanation
Suppose that:
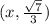
Then, we can build the following:
Then, as we know that the coordinates of the unis circle is (x=cos θ, y=sin θ), and we have the value of y, then we can solve for θ and then get cos θ.
0. Isolating for θ:
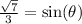
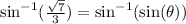
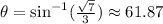
2. Calculating cos (θ):