Question

Hong received a $1700 bonus. He decided to invest it in a 5 year certificate of deposits (CD) with an annual interest rate of 1.53% compounded monthly.

Answer 1

Remember that

The compound interest formula is equal to

`A=P(1+(r)/(n))^(nt)`

where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is the number of Time Periods

n is the number of times interest is compounded per year

in this problem we have

P=$1,700

t=5 years

r=1.53%=1.53/100=0.0153

n=12

Part A

substitute the given values

`\begin{gathered} A=1,700(1+(0.0153)/(12))^(12*5) \\ \\ A=1,700(1.001275)^(60) \end{gathered}`

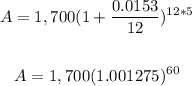
A=$1,835.06

therefore

The answer to Part A is $1,835.06

Part B'

Find out the interest

I=A-P

substitute given values

I=$1,835.06-$1,700

I=$135.06

The answer to Part B is $135.06