Answer:
Explanation:
The angle between two vectors is represented by the following equation:
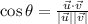
Notice that this equation involves a trigonometric function, the dot product of two vectors, and the magnitude of two vectors.
For v=<10,2>, w=<-5,-1>:
As a first step let's determine the dot product of the two vectors:
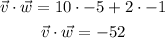
Then, calculate the magnitudes of the vectors:
![\begin{gathered} \lvert\vec{v}\rvert=\sqrt[]{(10)^2+(2)^2}=2\sqrt[]{26} \\ \lvert\vec{w}\rvert=\sqrt[]{(-5)^2+(-1)^2}=\sqrt[]{26} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u76dtmsn72utpsc0x581i40ikgm2sxv5un.png)
Now, substitute the values into the equation:
![\begin{gathered} \cos \theta=\frac{-52}{2\sqrt[]{26}\cdot\sqrt[]{26}} \\ \cos \theta=-1 \\ \theta=\cos ^(-1)(-1)=\text{ 180\degree} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ixdhpifmk05oia74339pd16sjv6lzcuozc.png)
For v=<3,1>, w=<2,-6>:
![\begin{gathered} \vec{v}\cdot\vec{w}=3\cdot2+1\cdot-6 \\ \vec{v}\cdot\vec{w}=0 \\ \lvert\vec{v}\rvert=\sqrt[]{(3)^2+(1)^2}=\sqrt[]{10} \\ \lvert\vec{w}\rvert=\sqrt[]{(2)^2+(-6)^2}=2\sqrt[]{10} \\ \cos \theta=\frac{0}{2\sqrt[]{10}\cdot\sqrt[]{10}} \\ \theta=\cos ^(-1)(0)=\text{ 90\degree} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zbyabon2mw23lnig6fp1wn4k4lf2ch3g47.png)
For v=<-10,5>, w=<1,-2>:
![undefined]()