Question

An airplane is flying at an altitude of 6000 m over the ocean directly toward acoastline. At a certain time, the angle of depression to the coastline from the airplaneis 14°. How much farther (to the nearest meter) does the airplane have to fly before itis directly above the coastline?O 5822 mO 1496 mO 1451 mO 24065 m

Answer 1

Step-by-step explanation

Using the data of the statement, we make the following diagram:

From the diagram, we see that:

• ΔPSC forms a right triangle,

,

• m∠C = θ = 14° is the angle of depression,

,

• oc = PS = 6000 m is the opposite side to angle θ,

,

• ac = SC = x is the adjacent side to angle θ.

From trigonometry, we have the relation:

`\tan\theta=(oc)/(ac)\Rightarrow ac=(oc)/(\tan\theta).`

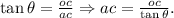
Replacing the data from above, we get:

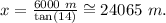
`x=\frac{6000\text{ }m}{\tan(14\degree)}\cong24065\text{ }m.`Answer

24065 m